Bài toán thuận của động học tay máy
Trong đại đa số các trường hợp, tay máy là một chuỗi động hở, được cấu tạo bởi một số khâu (Links), được nối với nhau nhờ các khớp. Một đầu của chuỗi nối với giá (Bơse), còn đầu kia nối với phần công tác. Mỗi khâu hình thành cùng với khớp phía trước nó một cặp khâu – khớp. Tuỳ theo kết cấu của mình mà mỗi loại khớp đảm bảo cho khâu nối sau nó các khả năng chuyển động nhất định.
Mỗi khớp (thực chất là cặp khâu – khớp) được đặc trưng bởi 2 loại thông số:
– Các thông số không thay đổi giá trị trong quá trình làm việc của tay máy được gọi là tham số.
– Các thông số thay đổi khi tay máy làm việc được gọi là các biến khớp.
Hai loại khớp thông dụng nhất trong kỹ thuật tay máy là khớp trượt và khớp quay. Chúng đều là loại khớp có một bậc tự do.
Bài toán thuận nhằm mô tả thế (vị trí và hướng) của phần công tác dưới dạng hàm số của các biến khớp. Giả sử có một tay máy với n+1 khâu và n khớp (hình 2.13). Thế của phần công tác so với hệ toạ độ gốc 
được mô tả bằng vector định vị p° và hướng của các vector chỉ phương n, s, a. Phép chuyển đổi toạ độ được biểu diễn bằng ma trận chuyển đổi thuần nhất:
Trong đó, q là vector n phần tử, gồm các biến khớp; p là vector định vị; n,, s, a là các vector chỉ phương của phần công tác, cũng chính là vector đơn vị của các trục toạ độ. Nếu phần công tác là tay gắp thì gốc tọa độ đặt vào tâm quay; vector a đặt theo phương tiến đến vật; s nằm trong mật phẳng trượt của hàm kẹp; n vuông góc với a và s theo quy tắc bàn tay phải.
Một trong những phương pháp giải bài toán thuận là dùng trực tiếp hình học giải tích. Ví dụ, đối với trường hợp cơ cấu 2 khâu phẳng (hình 2.14), ta có:
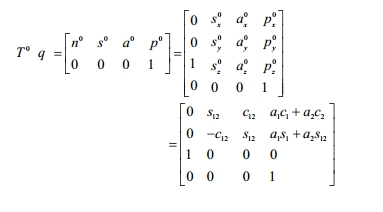
Phương pháp tính toán trực tiếp chỉ áp dụng được cho các cơ cấu đơn giản. Để có thể giải các bài toán tổng quát cần một thuật giải chung. Một trong những thuật giải như vậy xuất phát từ quy tắc Denavit-Hartenberg, được Denavit và Hartenberg xây dựng vào năm 1955. Đó là quy tắc thiết lập hệ thống toạ độ trên các cặp khâu – khớp trên tay máy. Dựa trên hệ toạ độ này có thể mô tả các cặp bằng hệ thống các tham số, biến khớp và áp dụng một dạng phương trình tổng quát cho bài toán động học tay máy.
1.4.1. Mô tả quy tắc Denavit-Hartenberg
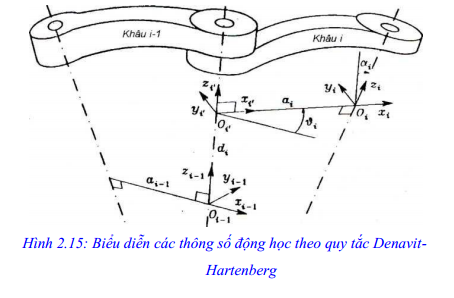
Giả sử trong chuỗi động học của tay máy có n khâu, khâu thứ i nối khớp thứ i với khớp thứ i+1 (hình 2.15).
Theo quy tắc Denavit-Hartenberg thì hệ toạ độ được gắn lên các khâu, khớp như sau:
– Đặt trục toạ độ Zj dọc theo trục của khớp sau (thứ i+1).
– Đặt gốc toạ độ Oi, tại giao điểm giữa zi và pháp tuyến chung nhỏ nhất của trục zi
Quy tắc Denavit-Hartenberg có một số trường hợp đặc biệt, cho phép đơn giản hoá thủ tục tính toán:
– Đối với hệ toạ độ gốc chỉ có phương của trục z0 là xác định. Gốc 0,1 và trục Xj có thể chọn tuỳ ý.
– Đối với hệ thứ n, chỉ có phương của trục Xị là xác định. Trục Zị có thể chọn tuỳ ý.
– Khi 2 khớp liền nhau có trục song song, vị trí của pháp tuyến chung có thể lấy bất kỳ.
– Khi trục của 2 khớp liền nhau có trục cắt nhau, phương của trục xi có thể chọn bất kỳ.
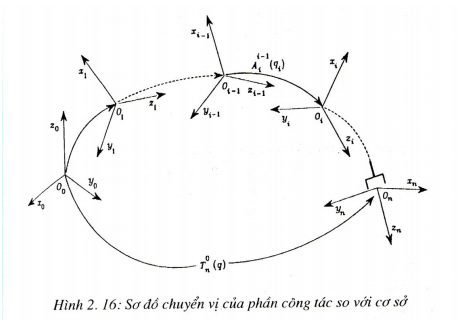
Một cách tổng quát, quy tắc Denavit-Hartenberg cho phép tổ hợp các ma trận chuyển vị riêng rẽ thành một ma trận chuyển vị thuần nhất, biểu diễn vị trí và hướng của khâu n so với khâu cơ sở.
Quy tắc này có thể áp dụng cho chuỗi hở bất kỳ trong kết cấu tay máy, như biểu diễn trong hình 2.16.
1.4.2. Một số ví dụ áp dụng quy tắc Denavit-Hartenberg
Cơ cấu 3 khâu phẳng
Cơ cấu có 3 khớp quay với các trục song song. Đặt trục Xi dọc theo phương của
các khâu, còn các tham số — ^ Các biến khớp là các góc quay ^. Sơ đồ động học và bảng tham số Denavit-Hartenberg như trên hình 2.17.
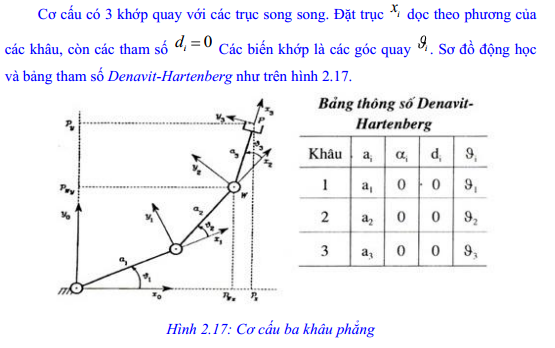
Vì các cặp khâu – khớp có kết cấu tương tự nhau, nên từ (2.34) có thể viết cả 3 ma trận chuyển đổi thuần nhất dưới dạng như nhau:
1.4.3. Vùng hoạt động của phần công tác
Như đã nói ở trên, vị trí của phần công tác được đại diện bởi vị trí của gốc toạ độ gắn trên nó so với hệ toạ độ chung, nghĩa là bởi vector p. Tương tự, hướng của phần cồng tác được mô tả thông qua bộ các tham số MRO và, một cách hình thức, ta biểu
Biểu thức này dùng một số lượng tối thiểu các thông số độc lập nhau để mô tả thế của phần công tác. Nó cũng biểu diễn vùng, trong đó tay máy có thể hoạt động theo đúng chức năng của nó, gọi là vùng hoạt động.
Vector n x 1 biểu diễn miền giá trị của các biến khớp ql , gọi là không gian khớp:
Đó cũng chính là trường hợp riêng của (2.37), biểu diễn vùng hoạt động của tay máy 3 khâu phẳng.
Một trong những thông số động học quan trọng của tay máy là vùng làm việc (Workspace) của nó. Đó là không gian mà gốc toạ độ của phần công tác có thể với tới được, tức là không tính đến sự định hướng của phần công tác. Đôi khi người ta phân biệt vùng làm việc nói trên (gọi là Reachable workspace) với vùng làm việc có tính đến sự định hướng của phần công tác (Dexterous Workspace).
Thể tích và hình dạng của vùng làm việc phụ thuộc vào kết cấu của tay máy và giới hạn (miền giá trị) của các biến khớp. Đối với tay máy có n bậc tự do, vùng làm việc là tập hợp mọi vị trí có thể của phần công tác, như mô tả trong phương trình động học:
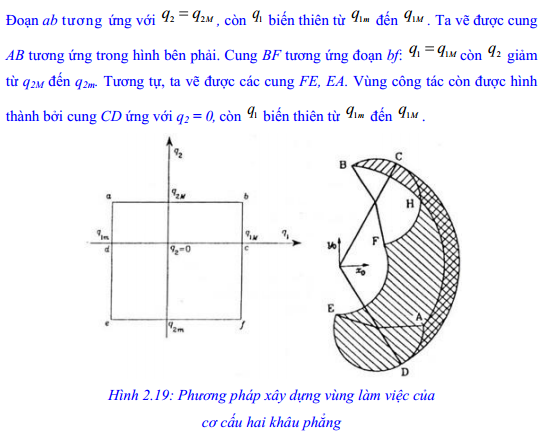
Biểu diễn hình học vùng công tác của tay máy là điều phức tạp. Tuy nhiên, chúng ta có thể hình dung về vùng làm việc của tay máy thông qua một ví dụ đơn giản. Đó là cơ cấu 2 khâu phẳng (hình 2.19).
Cấu hình và thế của cẳng tay được thể hiện bằng hình chữ nhật kín abcfeda.
1.5. Bài toán ngược của động học tay máy
Bài toán thuận của động học tay máy cho phép xác định thế của phần công tác và có thể cả vùng làm việc của nó theo quan hệ với các thông số động học của các cặp khâu – khớp. Bài toán ngược nhằm xác định bộ thông số động học để đảm bảo chuyển động cho trước của phần công tác. Theo biểu thức (2.34), nếu có bộ các thông số xác định thì có thề xác định 
một cách đơn trị. Đối với bài toán ngược thì không hẳn như vậy, vì:
– Các phương trình có dạng phi tuyến và siêu việt, thường không cho lời giải đúng.
– Có thể có nhiều lời giải.
– Có thể gặp nghiệm vô định, vì các liên kết thừa (giống như kết cấu siêu tĩnh).
– Có thể có nghiệm tìm được bằng toán học lại không chấp nhận được về mặt vật lý, do các ràng buộc về kết cấu.
Tính đa nghiệm của bài toán ngược không chỉ phụ thuộc vào số các biến khớp (tức là số bậc tự do) mà cả vào số lượng các tham số khác không trong kết cấu. Nói chung, số lượng này càng lớn thì số lời giải chấp nhận được càng nhiều. Ví dụ, tay máy số bậc tự do có thể có tới 16 nghiệm. Điều đó đòi hỏi phải có các điều kiện phụ về cơ cấu để giảm số nghiệm này.
Việc tìm kiếm một nghiệm phù hợp đòi hỏi ở người thiết kế một trực giác về toán học và về kết cấu để dự đoán những điểm hoặc khu vực khả dĩ giảm được số nghiệm cần chọn lựa.
1.5.1. Cơ cấu 3 khâu phẳng
Cơ cấu 3 khâu phẳng được hình dung như trong hình 2.17. So sánh phương trình động học của nó (2.35) với phương trình động học tổng quát (2.34) ta có thể xác định toạ độ của điểm W (gốc toạ độ của khớp 2) [3,tr.42]:
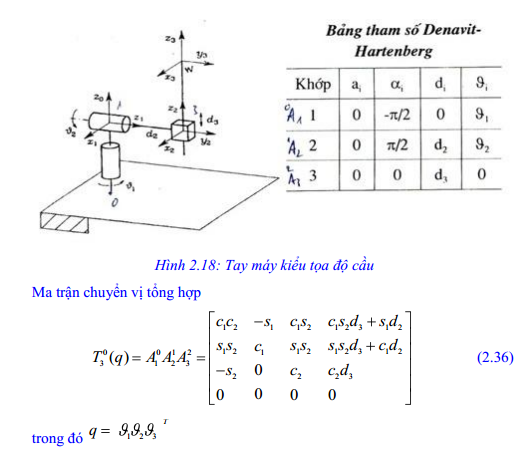
1.5.2. Cơ cấu cầu
